目的

给定控制点 $P_{i}(i=0,1,\cdots,n-1)$，构造一条依次通过点 $P_i$ 的曲线。

思路

类比贝塞尔曲线，令

$$P(t)=\sum_{i=0}^{n-1}P_if_{i,n}(t)$$

表示一条以 $t$ 为参数的曲线，其中 $t$ 的取值范围为 $\left(0,1-\frac 1n\right)$，且函数族 $f_{i,n}$ 满足

$$f_{i,n}\left(\frac jn\right)=\delta_{ij},\quad i,j\in{0,1,\cdots,n-1}$$

其中 $\delta_{ij}$ 为Kronecker $\delta$ 符号，故不难发现 $P\left(\frac in\right)=P_i$，即曲线 $P(t)$ 依次通过点 $P_i$。下面寻找合适的函数族 $f_{i,n}$。

理论推导

我们希望找到一个函数 $f$，满足以下性质：

$$f(0)=1,\quad f\left(\frac1n\right)=f\left(\frac2n\right)=\cdots=f\left(\frac{n-1}n\right)=0 \tag{1}$$

那么，令 $f_{i,n}(t)=f\left(t-\frac{i}n\right)$，则有 $f_{i,n}\left(\frac jn\right)=f\left(\frac{j-i}n\right)=\delta_{ij}$。

尝试令 $f(t)=C+\sum\limits_{k=1}^{m}A_k\cos (2\pi k t)$，其中阶数 $m$ 待定，则易见函数 $f$ 具有以下性质：①周期为1；②是偶函数。因此，$t=\frac12$ 也是 $f$ 的一条对称轴，从而当 $n$ 为偶数时，式(1)等价于

$$f(0)=1,\quad f\left(\frac1n\right)=f\left(\frac2n\right)=\cdots=f\left(\frac12\right)=0\tag{2}$$

共 $\frac n2+1$ 个方程，故应令 $m=\frac n2$；当 $n$ 为奇数时，式(1)等价于

$$f(0)=1,\quad f\left(\frac1n\right)=f\left(\frac2n\right)=\cdots=f\left(\frac{n-1}{2n}\right)=0\tag{3}$$

共 $\frac {n+1}2$ 个方程，故应令 $m=\frac {n-1}2$。通过求解式(2)或(3)中的方程组解出参数 $A_k$ 和 $C$，就可以得到函数 $f$ 的解析式。

权重性质

从曲线 $P(t)$ 的定义式可以看出，对某个固定的 $t$，$P(t)$ 是所有 $P_i$ 坐标的加权平均，权重为 $f_{i,n}(t)$。下面证明，采用上一部分的 $f_{i,n}(t)$ 定义，则所有权重的和恒为 $1$，即 $\sum\limits_{i=0}^{n-1}f_{i,n}(t)\equiv1$：

令 $g(t)=\sum\limits_{i=0}^{n-1}f_{i,n}(t)=\sum\limits_{i=0}^{n-1}f\left(t-\frac{i}n\right)$，则 $g(0)=1$，且

$$\begin{aligned}\frac{\mathrm{d}}{\mathrm{d} t}g(t)&=\sum_{i=0}^{n-1}\frac{\mathrm{d}}{\mathrm{d} t}f\left(t-\frac in\right)\\ &=-\sum_{i=0}^{n-1}\sum_{k=1}^m 2\pi kA_k\sin\left[2\pi k\left(t-\frac in\right)\right]\\ &=-\sum_{k=1}^m2\pi kA_k\sum_{i=0}^{n-1}\sin\left[2\pi k\left(t-\frac in\right)\right]\end{aligned} \tag{4}$$

注意到三角恒等式

$$\begin{aligned}\sum_{i=0}^{n-1}\sin\left(\theta-2\pi k \frac in\right)&=\frac{1}{2\mathrm{j}}\sum_{i=0}^{n-1}\exp \left[\mathrm{j}\left(\theta-2\pi k \frac in\right)\right]-\frac{1}{2\mathrm{j}}\sum_{i=0}^{n-1}\exp\left[-\mathrm{j}\left(\theta-2\pi k \frac in\right)\right]\\ &=\frac{1}{2\mathrm{j}}\frac{\mathrm{e}^{\mathrm{j}\theta}\left[1-\exp\left(-\mathrm{j}2\pi ki\right)\right]}{\exp\left(-\mathrm{j}2\pi k\frac in\right)}-\frac{1}{2\mathrm{j}}\frac{\mathrm{e}^{-\mathrm{j}\theta}\left[1-\exp\left(\mathrm{j}2\pi ki\right)\right]}{\exp\left(\mathrm{j}2\pi k\frac in\right)}\\ &=0\end{aligned}$$

取 $\theta=2\pi kt$ 代入(4)，即得 $\frac{\mathrm{d}}{\mathrm{d} t}g(t)=0$，从而 $g(t)\equiv 1$，即 $f_{i,n}(t)$ 是一组归一化的权值系数。

$A_k$ 与 $C$ 的解析解

实际上，可以给出 $A_k$ 和 $C$ 的解：

$$(C,A_1,A_2,\cdots, A_m)=\begin{cases}\left(\frac1{n},\frac2n,\frac2n,\cdots,\frac2n,\frac1{n}\right),\quad n\text{为偶数} \\ \left(\frac1{n},\frac2n,\frac2n,\cdots,\frac2n\right),\quad n\text{为奇数}\end{cases}$$

如果再注意到上式中大部分系数相同，那么理论上就可以应用公式

$$\sum\limits_{k=1}^n\cos(\theta+k\varphi)=\begin{cases}\frac{\cos\left(\theta+\frac12\varphi\right)-\cos\left[\theta+\left(n+\frac12\right)\varphi\right]}{2\sin\frac12\varphi},\quad \varphi\ne2k\pi,k\in\mathbb{Z}\\n\cos\theta,\quad\varphi=2k\pi,k\in\mathbb{Z}\end{cases}$$

来达到简化计算的目的。

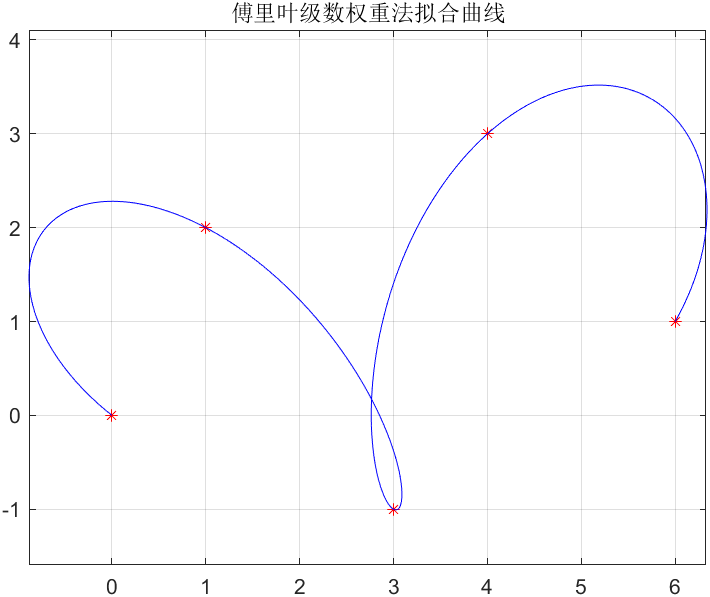
曲线生成效果

下面是控制点坐标如下表所示时该算法生成的曲线：

代码

代码中未应用式(5)及其优化。

clear all;
controlPoints = [0, 0; 1, 2; 3, -1; 4, 3; 6, 1];

n = size(controlPoints, 1);

t = 0:0.01:n-1;
x = zeros(size(t));
y = zeros(size(t));

% 计算傅里叶系数
coeff = GetFourierCoefficient(n);

for i = 1:n
    % 计算第i个控制点的权重
    weight = GetFourierWeight(coeff, t, i - 1, n);
    % 计算第i个控制点的x坐标
    x = x + weight * controlPoints(i, 1);
    % 计算第i个控制点的y坐标
    y = y + weight * controlPoints(i, 2);
end

% 画出控制多边形
plot(controlPoints(:, 1), controlPoints(:, 2), 'r*');
hold on; grid on; axis equal;

% 画出拟合的曲线
plot(x, y, 'b-');
title('傅里叶级数权重法拟合曲线')

function coeff = GetFourierCoefficient(n)
    if mod(n, 2) == 0
        A = zeros(n / 2 + 1, n / 2 + 1);
        b = zeros(n / 2 + 1, 1);
        b(1) = 1;
        for i = 0:n / 2
            A(i + 1, :) = cospi(2 * i * (0:n / 2) / n);
        end
        coeff = A \ b;
    else
        A = zeros((n + 1) / 2, (n + 1) / 2);
        b = zeros((n + 1) / 2, 1);
        b(1) = 1;
        for i = 0:(n - 1) / 2
            A(i + 1, :) = cospi(2 * i * (0:(n + 1) / 2 - 1) / n);
        end
        coeff = A \ b;
    end
end

function weight = GetFourierWeight(coeff, t, k, n)
    if mod(n, 2) == 0
        weight = coeff(1) * ones(size(t));
        for i = 1:n / 2
            weight = weight + coeff(i + 1) * cospi(2 * i * (t - k) / n);
        end
    else
        weight = coeff(1) * ones(size(t));
        for i = 1:(n - 1) / 2
            weight = weight + coeff(i + 1) * cospi(2 * i * (t - k) / n);
        end
    end
end